Programación Lineal con Python
La programación lineal es una técnica de optimización de una función lineal objetivo con restricciones. Se trata de hallar el mejor resultado en un modelo matemático representado a través de ecuaciones lineales.
Según la página de Google Developers (enlace: Combinatorial Optimization Overview) la optimización combinatoria es una forma de hallar la mejor solución en un conjunto muy grande pero finito de soluciones posibles. Entre los problemas que se puden solucionar con este procedimiento están:
- Optimización (programación) lineal: se busca hallar la mejor solución a un problema dado un grupo de relaciones lineales.
- El vendedor (agente) viajero: dada una lista de ciudades y las distancias entre ellas ¿Cómo encontrar la ruta más corta que recorra todas las ciudades?
- El problema de la mochila (knapsack problem): dado un número determinado de objetos con un peso y valor ¿Cómo escoger los objetos para empacarlos en una mochila de modo que se minimice el peso y se maximice el valor?
- El problema de las ocho reinas (N-Queen problem): ¿Cómo ubicar 8 reinas en un tablero de ajedrés de modo que no se amenacen entre sí?
- Resolver un sudoku: ubicar dígitos en una grilla de manera que no se repitan en determinada columna o fila.
Con el módulo or-tools de Google podemos resolver problemas de programación lineal. or-tools usa la herramienta Glop (Google’s linear programming system) a través de un wrapper llamado pywraplp
Ejemplo de aplicación:
La empresa Banner produce sustancias químicas industriales. Tiene la capacidadde producir por semana 110 barriles de lubricante que viene en dos presentacions: Regular y Supremo. Ambas variantes requieren dos aditivos pero en proporciones diferentes. El Regular contiene 3 galones de aditivo A y un galón de aditivo B por barril mientras el Supremo contiene 2 galones de A y 3 de B por barril.
En una semana determinada sólo hay 300 galones de aditivo A y 280 de aditivo B. Un barril de Regular produce $80 de ganancia y un barril de Supremo genera una ganancia de $200.
¿Cuántos barriles de cada químico se deben producir por semana?
| Regular | Supremo | Disponible | |
|---|---|---|---|
| Aditivo A | 3 gal | 2 gal | 300 gal |
| Aditivo B | 1 gal | 3 gal | 280 gal |
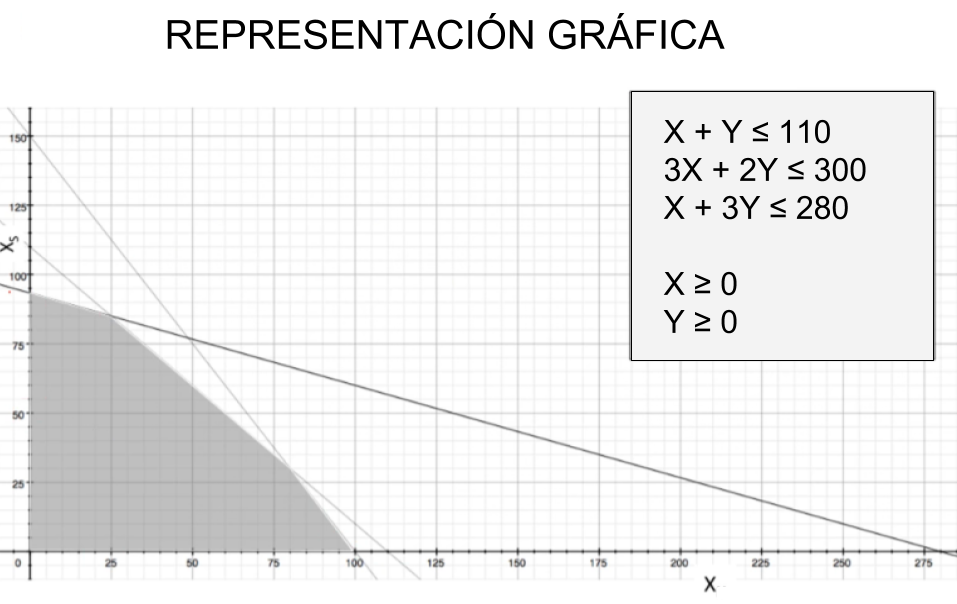
Si x es el número de barriles de Regular y y el número de barriles de Supremo, se trata de hallar x y y que maximicen la suma \(80 x + 200 y\) (ganancia) sujeta a las restricciones:
\[x + y \leq 110\] \[3 x + 2 y \leq 300\] \[x + 3 y \leq 280\]Aquí se tienen dos incógnitas y tres restricciones y el código para hallar la respuesta es:
from __future__ import print_function
from ortools.linear_solver import pywraplp
def main():
# Se crea un Glop solver llamado EjemploLineal.
solver = pywraplp.Solver('EjemploLineal',
pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)
# Se crean las dos variables x, y
x = solver.NumVar(-solver.infinity(), solver.infinity(), 'x')
y = solver.NumVar(-solver.infinity(), solver.infinity(), 'y')
# Restricción 1: x + y <= 110.
restriccion1 = solver.Constraint(-solver.infinity(), 110)
restriccion1.SetCoefficient(x, 1)
restriccion1.SetCoefficient(y, 1)
# Restricción 2: 3x + 2y <= 300.
restriccion2 = solver.Constraint(-solver.infinity(), 300)
restriccion2.SetCoefficient(x, 3)
restriccion2.SetCoefficient(y, 2)
# Restricción 3: x + 3y <= 280.
restriccion3 = solver.Constraint(-solver.infinity(), 1)
restriccion3.SetCoefficient(x, 1)
restriccion3.SetCoefficient(y, 3)
# Función Objetivo: 80x + 200y.
objective = solver.Objective()
objective.SetCoefficient(x, 80)
objective.SetCoefficient(y, 200)
objective.SetMaximization()
# Resolver el sistema.
solver.Solve()
opt_solution = 80 * x.solution_value() + 200 * y.solution_value()
print('Numero de variables =', solver.NumVariables())
print('Numero de restricciones =', solver.NumConstraints())
# El valor de cada variable en la solucion.
print('Solución:')
print('x = ', round(x.solution_value()))
print('y = ', round(y.solution_value()))
# El valor objetivo de la solución.
print('Valor objetivo óptimo = ', opt_solution)
if __name__ == '__main__':
main()Luego de ejecutar el script tenemos la salida:
Numero de variables = 2 Numero de restricciones = 3 Solución: x = 25 y = 85 Valor objetivo óptimo = 19000