Regresión Lineal con Pandas: método del gradiente

El curso de aprendizaje automático (machine learning) de Andrew Ng en Coursera es muy popular y es una buena introducción a este tema. En su curso, Ng recomienda usar Matlab u Octave para los ejercicios de programación. Uno de estos ejercicios pide hallar la curva de ajuste lineal de una serie de datos.
In this exercise, you will implement linear regression and get to see it work on data. Before starting on this programming exercise, we strongly recommend watching the video lectures and completing the review questions for the associated topics. To get started with the exercise, you will need to download the starter code and unzip its contents to the directory where you wish to complete the exercise. If needed, use the cd command in Octave/MATLAB to change to this directory before starting this exercise. You can also find instructions for installing Octave/MATLAB in the “Environment Setup Instructions” of the course website.
El método del gradiente (gradient descent en inglés) en regresión lineal permite obtener la curva de ajuste de una función de forma iterativa minimizando la función costo:
\[J(\theta) = \frac{1}{2m}\sum_{i=1}^mh_{\theta}((x^{(i)}) - y^{(i)})^{2}\]La hipótesis \(h_{\theta}(x)\) está dada por el modelo lineal:
\[h_{\theta}(x) = \theta^{T}x = \theta_{0} + \theta_{1}x_{1}\]El ajuste se logra cambiando los valores \(\theta_{j}\) con el método del gradiente en el que en cada iteración se actualiza ese valor:
\[\theta_{j} := \theta_{j} - \alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})x_{j}^{(i)}\]Donde \(\alpha\) es la tasa de aprendizaje. A continuación se muestra la implementación de este método usando los módulos pandas y numpy de python y la visualización con matplotlib.
El algoritmo que se usa queda de la siguiente forma para theta0 y theta1: repetir hasta que se alcance convergencia
\[\theta_{0} := \theta_{0} - \alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})\] \[\theta_{1} := \theta_{1} - \alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})x^{(i)}\]El archivo con los datos se puede ver aquí: ex1data1.txt
# Implementación del método del gradiente con pandas
# Datos del curso de Andrew Ng de aprendizaje automático
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
archivo = 'ex1data1.txt'
df = pd.read_csv(archivo, header=None, names=['poblacion', 'ganancia'])
df.head()
poblacion ganancia
0 6.1101 17.5920
1 5.5277 9.1302
2 8.5186 13.6620
3 7.0032 11.8540
4 5.8598 6.8233
def calc_costo(dframe, th0, th1):
""" Calcula el costo J """
poblacion = dframe['poblacion']
prediccion = poblacion * th1 + th0
ganancia = dframe['ganancia']
return np.sum(np.square((prediccion - ganancia)) / len(dframe) / 2.0
def grad_desc(dframe, th0, th1, alpha):
""" Implementa un paso en el algoritmo de descenso en gradiente """
length = len(dframe)
dframe['prediccion'] = dframe['poblacion'] * th1 + th0
th0 = th0 - alpha / length * np.sum((dframe['prediccion'] - dframe['ganancia']))
th1 = th1 - alpha / length * np.sum(((dframe['prediccion'] - dframe['ganancia']) * dframe['poblacion']))
return th0, th1Implementación y gráfica luego de 200 iteraciones:
def test_graph(df, iteraciones):
""" implementa el método del descenso en el dataframe """
theta0, theta1 = 0, 0
alpha = 0.01
for elem in range(iteraciones):
theta0, theta1 = grad_desc(df, theta0, theta1, alpha)
costo = calc_costo(df, theta0, theta1)
plt.plot(df['poblacion'], df['ganancia'], 'b.', df['poblacion'], df['poblacion']*theta1 + theta0, 'r-')
plt.title('Método del gradiente con pandas')
plt.xlabel('Población')
plt.ylabel('Ganancia')
plt.text(5, 23, 'Costo: {}'.format(costo))
plt.text(5, 19, 'theta0: {}\ntheta1: {}\niteraciones: {}'.format(theta0, theta1, iteraciones))
plt.show()
test_graph(df, 200)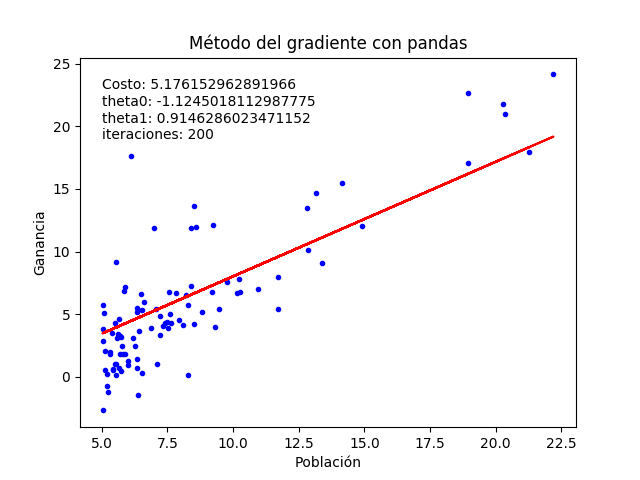
Graficamos la función costo al avanzar el número de iteraciones para observar como se va acercando a un valor mínimo:
def plot_with_cost(df, iteraciones):
""" Calcula el costo por cada iteración """
valores_costo = []
theta0, theta1 = 0, 0
for elem in range(iteraciones):
theta0, theta1 = grad_desc(df, theta0, theta1, alpha)
costo = calc_costo(df, theta0, theta1)
valores_costo.append(costo)
plt.plot(range(iteraciones), valores_costo)
plt.show()
plot_with_cost(df, 1500)Y esta es la gráfica del cambio del costo a medida que transcurren las iteraciones:
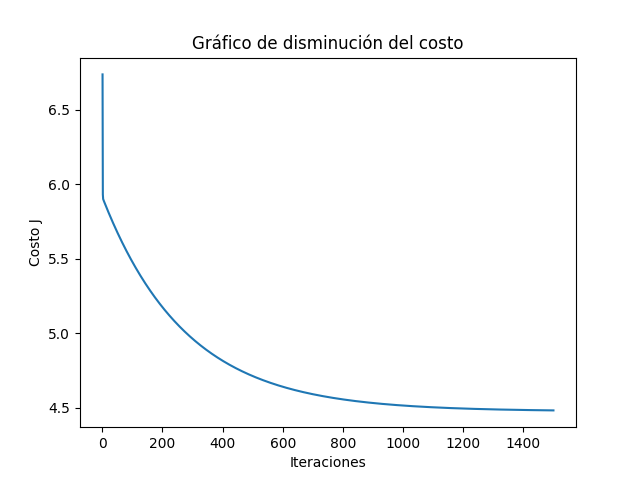
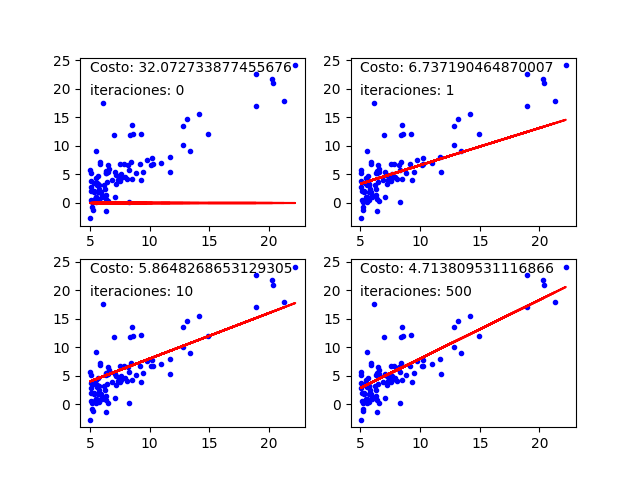
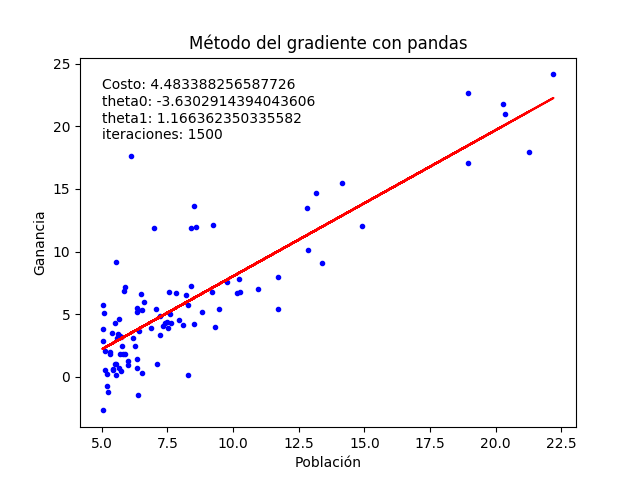
Según la gráfica se necesitan cerca de 1500 iteraciones para hallar un ajuste óptimo. Usando ese valor obtenemos una mejor gráfica de la función lineal que se ajusta a los datos:
Finalmente podemos ver la evolución de la curva de ajuste y de la función costo a medida que se ejecutan las iteraciones: